Know Your Wisdom

DH 密钥交换算法

2022-04-09

这篇文章主要介绍 DH 密钥交换算法，涉及：

  1. 密钥交换相关的数学原理，模运算，欧拉定理
  2. 使用 python 写一个 DH 密钥交换算法
  3. 证明为什么离散对数问题是安全的

问题背景及目标

通信模型
通信模型
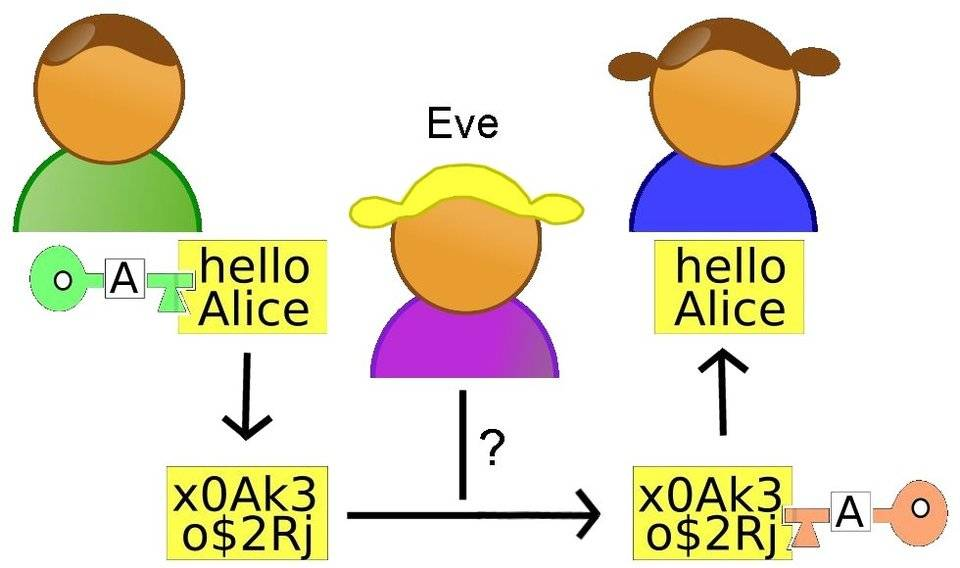
  1. Alice 和 Bob 要通过中间人 Eve 进行通信
  2. Eve 会监听他们俩的通信内容，但是不会修改

如何才能保证通信安全？即内容对 Eve 不可见

Diffie–Hellman key exchange

缺点：无法抵挡中间人攻击、Logjam 攻击

Terminology

互质

（1）两个不同的质数一定是互质数

（2）一个质数，另一个不为它的倍数，这两个数为互质数

（3）1不是质数也不是合数，它和任何一个自然数（1本身除外）在一起都是互质数。如1和9908

（4）相邻的两个自然数是互质数。如 15与 16。

（5）相邻的两个奇数是互质数。如 49与 51。

（6）较大数是质数的两个数是互质数。如97与88。

欧拉函数 φ(n)

在数论中，对正整数n，欧拉函数 是小于或等于n的正整数中与n互质的数的数目。

欧拉定理

欧拉定理
欧拉定理

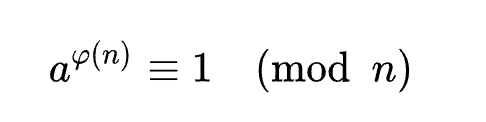
举例：a=3，n=5，则 φ(n)=φ(5)=4。

那么就有 aφ(n) = a4 = 81，81 % 5 = 1

原根

在欧拉公式中，已知 n 和 φ(n)，求一个特殊的 a 和 k (k <= φ(n)) 使得 ak = 1 % n 成立，且最小的 k = φ(n)，则最终求得的这个 a 就是 n 的原根。

注意：当 n 为质数时，φ(n)=(n-1)

例如 n=7，φ(n)=6，当 a=3 时，a6=1 % 7，则 a=3 为 n 的一个原根

例如 n=18，φ(n)=6， 5, 7 为 n 的原根

可以用下面的代码计算原根：

n = 18
phi_n = 6

def find_primitive_root(n, phi_n):
    ret = []
    for a in range(1, 18):
        for k in range(1, phi_n + 1):
            if a ** k % n == 1:
                if k != phi_n:
                    break
                else:
                    ret.append((a, k))
    return ret

print(f'finding primitive root for n={n}, phi_n={phi_n}:')
for a, k in find_primitive_root(n, phi_n):
    print(f'found a={a:<3d}, k={k:<3d}')

Output:

finding primitive root for n=18, phi_n=6:
found a=5  , k=6  
found a=11 , k=6

密钥交换流程

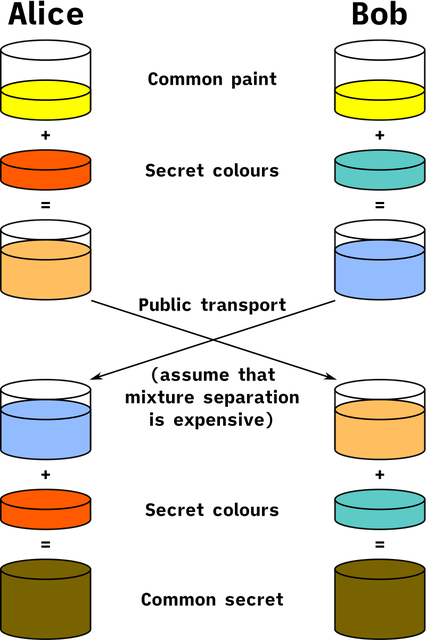
DH 密钥交换算法
DH 密钥交换算法

Alice 和 Bob 各自贮藏了一个随机生成的私钥 a, b，然后在 public transport 之前用上面的欧拉定理进行计算（加密）得到 A B 两个安全的公钥。最后再次通过欧拉定理进行计算，此处得到 B**a % n = A**b % n = priv_key，这里计算得到的就是私钥 priv_key，也就是图中灰色的部分。

公私钥混合得到共享密钥
公私钥混合得到共享密钥

用 python 实现

class KeyExchange:
    p: int
    g: int

    def __init__(self, p, g, secret_key=None):
        self.p, self.g = p, g
        self.secret_key = secret_key

    def get_middle_public_key(self, secret_key: int=None):
        secret_key = secret_key or self.secret_key
        assert secret_key is not None
        return self.g ** secret_key % self.p

    def get_shared_key(self, middle_public_key: int, secret_key: int=None):
        secret_key = secret_key or self.secret_key
        assert secret_key is not None
        return middle_public_key**secret_key % self.p

# Alice and Bob are preparing for communication
p, g = 23, 5
alice = KeyExchange(p, g, 4)
bob = KeyExchange(p, g, 3)

# Eve can get below middle public key
alice_pub_key = alice.get_middle_public_key()
bob_pub_key = bob.get_middle_public_key()
print('alice pub key:', alice_pub_key)
print('bob pub key:', bob_pub_key)

# Alice and Bob got same shared key
alice_shared_key = alice.get_shared_key(bob_pub_key)
bob_shared_key = bob.get_shared_key(alice_pub_key)
assert alice_shared_key == bob_shared_key, 'alice={},\nbob={}'.format(alice_shared_key, bob_shared_key)
print('shared key is:', alice_shared_key)

Output:

alice pub key: 4
bob pub key: 10
shared key is: 18

通过修改 p, g 参数和 alice / bob 的 secret key，可以得到不同的 shared key

离散对数问题的安全性

pub_key = g**secret_key % p

这里 eve 已知上式中的 g / p / pub_key，求 secret_key。

这里 p 是一个非常大的数字，由于取模指数的 log 函数非常难求，所以 secret key 是相对安全的。

Catalogue